Для некоторых целей нам будет удобно использовать другое определение, известное как определение предела функции «по Гейне». Оно основано на понятии предела последовательности. Это определение эквивалентно предыдущему это мы чуть позже докажем и хорошо согласуется с интуицией: например, на картинках в разделе примеры и мотивировка предыдущей лекции мы рисовали как раз последовательности значений x , и показывали чисто визуально , что последовательность соответствующих значений функции стремится к нужному нам числу. Из Коши следует Гейне.

Конев В.В. Пределы последовательностей и функций

Последний раз редактировалось Deggial Необходимо доказать, что предела не существует. Я уже не много интересовался этим вопросом и выяснил что существует два способа доказательства: найти односторонние пределы справа, слева от точки как-то использовать последовательность В целях самообразования: всё ли я выше верно изложил может есть ещё способы? И вот три примера, в которых нужно доказать что предела не существует: , , , в каком примере какой способ использовать?

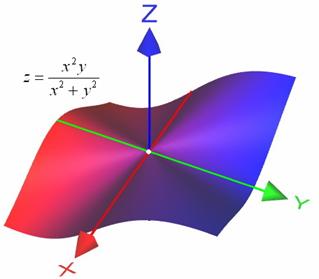
Если доказуемо никакой предел не существует, то undefined возвращен. Смотрите Пример 2. Если нельзя определить, существует ли предел или не может определить свое значение, то символьное limit возвращен. Смотрите Пример 3. То же самое содержит, в случае, если опция Intervals дан, если никакая информация на съемочной площадке предельных точек не могла бы быть получена.

• Высшая математика — просто и доступно! Наш форум, библиотека и блог: mathprofi.
• Конев В.
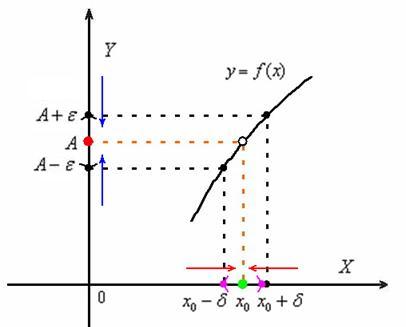
• Точный смысл термин «предел» имеет лишь при наличии корректного понятия близости между элементами точками множества, в котором указанная переменная принимает значения. Основные понятия математического анализа — непрерывность , производная , интеграл — определяются с помощью предела.
• Попробуйте повторить позже.
• Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
• Однако такого интуитивного понимания в более сложной ситуации может оказаться недостаточно.

Конев В. Пределы последовательностей и функций. Разделы курса Примеры Калькулятор. Дифференцирование Неопределенные интегралы Определенные интегралы Несобственные интегралы. Предел функции.

Похожие статьи

• Миниатюрный приёмник своими руками - Перила из дерева для деревянного крыльца, как сделать
• Когда стал желудок что делать как снять содой и лимонкой
• Сделать ящик для комода
• Электрический теплый пол своими руками на деревянных полах - Как сделать теплый пол в деревянном дом